Decision Tree Algorithm Explained .
Decision Trees is a supervised learning Algorithm used to solve classification and regression problems . The goal is to create a model that predicts the value of a target variable by learning simple decision rules taken from the data features.
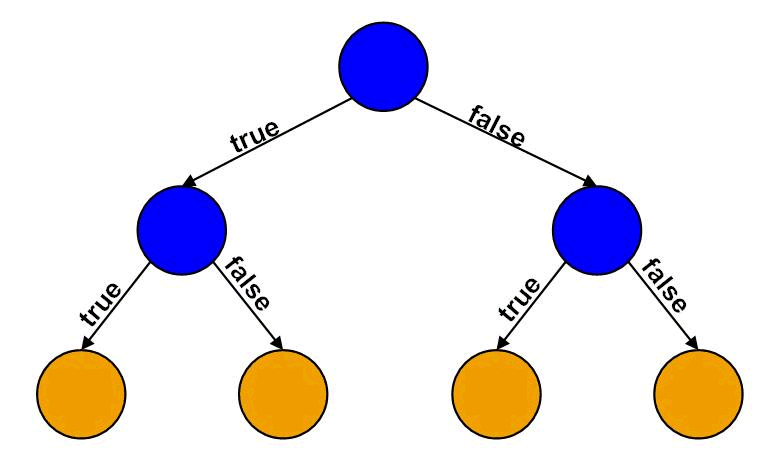
The idea behind Decision Tree is very simple , we try to find The best Feature and threshold that will split our data so that :
- The samples that they’ve feature value less than threshold will be stored in the left side .
- The samples that they’ve a feature value more than threshold will be stored in the right side .
- if a node is leaf , we will store the value of the class which is the most common class in the samples in this node .
We choose The Feature that will split our data Based on The Information gain , the feature that have to maximum value of the Information gain is the most Important. to calculate the Information gain we need first to calculate The Entropy for every Feature , the Formula of the Entropy is defined as following:
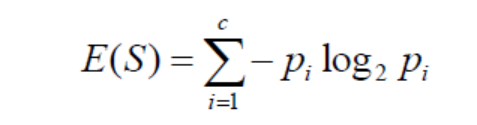
Now we can Calculate The Information Gain using this Formula :
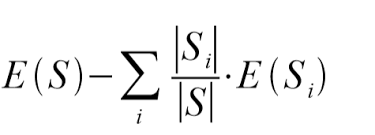
Implementation :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
import numpy as np
from collections import Counter
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
class Node :
"""
Node Takes 5 parameters
feature : the feature used to split in this Node
threshold : the threshold used to split in this Node
left : left Child of this Node
right : right Child of This Node
value : the Common class in This Node in case if he's a leaf Node
"""
def __init__(self , feature = None , threshold = None , left = None , right = None , value = None):
self.feature = feature
self.threshold = threshold
self.left = left
self.right = right
self.value = value
#Function Used to verify if a node is leaf or Not
def isLeafNode(self):
return self.value is not None
class DecisionTree :
"""
Decision Tree takes 3 parameters
min_Samples_to_Split : the Minimum Samples required to do a split
maximum_Depth : maximum depth of a tree
nbr_features : the number of features in a tree
"""
def __init__(self , min_Samples_to_Split = 2 , maximum_Depth = 100 , nbr_features = None):
self.min_Samples_to_Split = min_Samples_to_Split
self.maximum_Depth = maximum_Depth
self.nbr_features = nbr_features
self.root = None
#Function Used to fit The Data to The Tree
def fit(self , x , y ):
self.nbr_features = x.shape[1] if self.nbr_features is None else min(self.nbr_features , x.shape[1])
self.root = self.GrowTree(x,y)
#a recursive Function used to add new Node based on a feature and a threshold to split
def GrowTree(self , x , y , depth = 0):
nbr_samples , nbr_features = x.shape
"""
np.unique it a numpy array that gives as unique values in an array
example :
a = np.array([1,1,1,2,2,3])
np.unique(a) return => [1,2,3]
"""
nbr_classes = len(np.unique(y))
"""
The Stop Criteria contains three conditions :
* Number Of Samples less than minimum samples to split (in our case is 2).
* depth greather than or equal the maximum depth (in our case is 100).
* Number of classes in a node is 1 , so we don't need to split the data .
"""
if (nbr_samples < self.min_Samples_to_Split or depth >= self.maximum_Depth or nbr_classes == 1 ):
leafValue = self.getMostCommonClass(y)
return Node(value=leafValue)
else :
#get The list of features in an array in a random way
features_Indexes = np.random.choice(nbr_features , self.nbr_features , replace = False)
#get The Best Feature and The Best Threshold to split the data using Greedy Search
bestFeature , bestThreshold = self.bestCriteria(x , y , features_Indexes)
#Now we've our best Feature to split the data and The Best Threshold
leftIndexes , rightIndexes = self.split(x[:,bestFeature] , bestThreshold)
#call the function GrowTree recursively
leftChild = self.GrowTree(x[leftIndexes,:], y[leftIndexes] , depth+1)
rightChild = self.GrowTree(x[rightIndexes,:], y[rightIndexes] , depth+1)
return Node(feature=bestFeature , threshold=bestThreshold , left=leftChild , right=rightChild )
"""
This Function used to get The Most Common label :
a = np.array([1,1,1,2,2,3,2,1,2])
common = Counter(a).most_common(1) => return ([1,4])
to get The most Common lable we do this => common:Label = common[0][0]
"""
def getMostCommonClass(self , y):
return Counter(y).most_common(1)[0][0]
"""
This Function is Used To Get The Best Feature and The Best threshold to split The Data
Using Greedy Search .
"""
def bestCriteria(self , x , y , featuresIndexes):
bestInformationGain = -1
split_Index , split_Threshold = None , None
for FeatureIndex in featuresIndexes:
xi = x[:,FeatureIndex]
thresholds = np.unique(xi)
for thresh in thresholds:
#Calculate The Information Gain if we split using This Feature and this threshold
CurrentInformationGain = self.informationGain(xi , y , thresh)
if CurrentInformationGain > bestInformationGain :
bestInformationGain = CurrentInformationGain
split_Index = FeatureIndex
split_Threshold = thresh
return split_Index , split_Threshold
"""
This Function Used to calculate The Information Gain Using This Formula :
Information_Gain = Entropy(Parent) - [Weighted Average of child i] * entropy(child i)
"""
def informationGain(self , x , y , threshold):
parentEntropy = self.entropy(y)
#Now we Need to split the data to find The left and right children
left_indexes , right_indexes = self.split(x , threshold)
parentSize = len(y)
leftSize , rightSize = len(left_indexes) , len(right_indexes)
leftWeightAVG , rightWeightAVG = leftSize / parentSize , rightSize / parentSize
leftEntropy , rightEntropy = self.entropy(y[left_indexes]) , self.entropy(y[right_indexes])
#Information_Gain = Entropy(Parent) - [Weighted Average of child i] * entropy(child i)
Information_Gain = parentEntropy - (leftWeightAVG * leftEntropy + rightWeightAVG * rightEntropy)
return Information_Gain
"""
This Function Used to Calculate The Entropy for a Node Using This Formula :
entropy = - Sigma ( (probability of X) * log2 (probability of X) )
"""
def entropy(self , y):
NumberOfOccurances = np.bincount(y)
probabilities = NumberOfOccurances / len(y)
return - np.sum([probability * np.log2(probability) for probability in probabilities if probability > 0])
"""
This Function Used to split The Data using a threshold passed in the parameters.
"""
def split(self , x , thresh):
left_indexes , right_Indexes = np.argwhere(x <= thresh).flatten() , np.argwhere(x > thresh).flatten()
return left_indexes , right_Indexes
"""
This Function Used To Predict a new Sample.
"""
def predict(self , x):
return np.array([self.traverseTree(xi , self.root) for xi in x])
"""
This Function Used to traverse The Tree .
"""
def traverseTree(self , x , node):
if node.isLeafNode():
return node.value
if x[node.feature] < node.threshold :
return self.traverseTree(x, node.left)
return self.traverseTree(x, node.right)
Testing The Model :
1
2
3
4
5
6
7
8
9
10
def accuracy(y_true , y_pred):
return np.sum(y_true == y_pred ) / len(y_true)
x , y = make_blobs(n_samples=100 , n_features=10 , centers=10 , random_state=0)
x_train , x_test , y_train , y_test = train_test_split(x,y,test_size=0.1)
decisionTree = DecisionTree(nbr_features=x_train.shape[1])
decisionTree.fit(x_train, y_train)
y_hat = decisionTree.predict(x_test)
print("Model Accuracy : ",accuracy(y_test, y_hat))