Linear Regression Algorithm Explained .
Linear regression is a linear approach for modelling the relationship between X and Y , where X is The Input Data and Y is The Target .
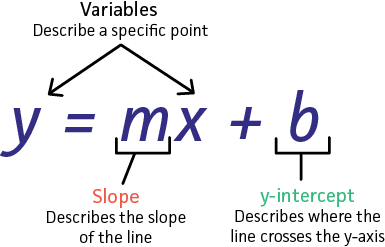
So linear regression consists of finding the coefficients m and b so that Y = m * X + b.
The Question now how can we find those coefficients :
-
we can try guess and check ??? (it not a good idea believe me) .
-
we can Use Gradient Descent to find them .
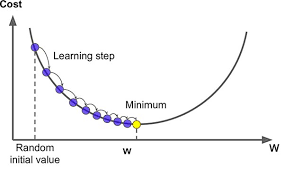
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function . [1]
The Cost Function Used in this Example is Log-Loss and it defined as following :
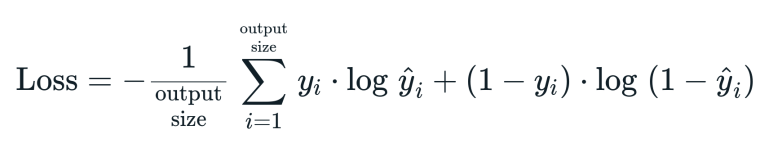
The Optimization Algorithm Used in this Example is Gradient Descent ans it defined as following :
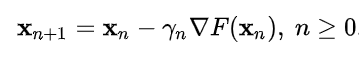
Implementation :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
class LinearRegression:
def __init__(self , learning_rate = 0.01 , nbr_iterations = 100):
self .learning_rate = learning_rate
self.nbr_iterations = nbr_iterations
def init_Parameters(self,x):
w , b = np.random.randn(x.shape[1]) , np.random.randn(1)
return w , b
def fit(self,x,y):
self.x_train = x
self.y_train = y
self.w , self.b = self.init_Parameters(self.x_train)
def gradient(self,y_hat):
dw = (1 / len(self.y_train)) * np.dot( -2 * self.x_train.T , (self.y_train - y_hat) )
db = (1 / len(self.y_train)) * -2 * np.sum(self.y_train - y_hat)
return dw , db
def train(self):
for i in range(self.nbr_iterations) :
y_hat = np.dot(self.x_train,self.w ) + self.b
dw , db = self.gradient(y_hat)
#Update The Weight and The Bias
self.w -= self.learning_rate * dw
self.b -= self.learning_rate * db
def predict(self , x):
y_hat = np.dot(x , self.w ) + self.b
return y_hat
def displayTheModel(self,x_test,y_test,y_hat):
plt.scatter(x_test , y_test , color='b')
plt.plot(x_test , y_hat , color='r')
plt.show()
Testing The Model :
1
2
3
4
5
6
7
8
9
10
11
12
13
def MSE(y_true , y_pred):
return 1 / len(y_true) * np.sum((y_true - y_hat) ** 2)
x , y = make_regression(n_samples=200 , n_features=1 , noise=0)
x_train , x_test , y_train , y_test = train_test_split(x,y , test_size=0.25)
L_Regression = LinearRegression()
L_Regression.fit(x_train, y_train)
L_Regression.train()
y_hat = L_Regression.predict(x_test)
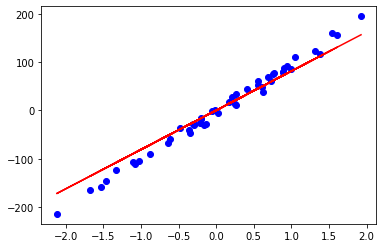
L_Regression.displayTheModel(x_test, y_test, y_hat)
print("MSE : ",MSE(y_test , y_hat))
The Model Result :