Support Vector Machines Algorithm Explained .
Support Vector Machine or SVM is a supervised learning Algorithm used for classification and regression problems. SVM can solve linear and non-linear problems , The idea behind SVM is very simple , the algorithm try to create a line that can separate the classes .
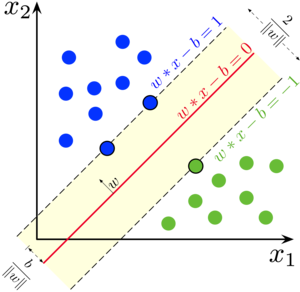
The goal of the line is to maximizing the margin between the points on either side of the so called decision line.
The Cost Function Used is This Example is defined as bellow :
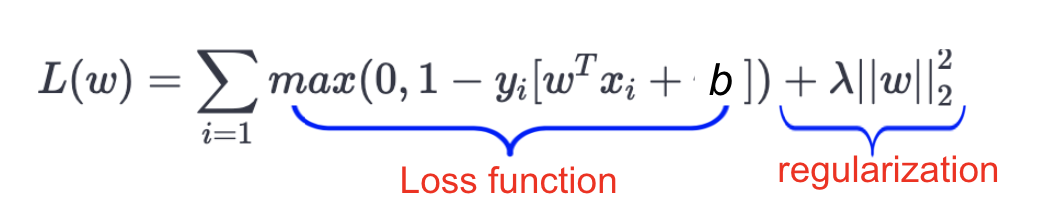
Implementation :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
class SVM :
def __init__(self , learning_rate = 0.01 , lambda_parameter = 0.01 , nbr_iteration = 1000):
self.learning_rate = learning_rate
self.lambda_parameter = lambda_parameter
self.nbr_iteration = nbr_iteration
def fit(self , x , y):
self.x_train = x
self.y_train = y #np.where(y<=0 , -1 , 1)
self.w , self.b = self.initParameters(x)
def initParameters(self , x):
w = np.random.randn(x.shape[1])
b = np.random.randn(1)
return w , b
def gradient(self,xi,yi,condition):
if condition :
dw = 2 * self.lambda_parameter * self.w
db = 0
return dw , db
else :
dw = 2 * self.lambda_parameter * self.w - np.dot(xi , yi)
db = yi
return dw , db
def train(self):
for i in range(self.nbr_iteration):
for index , xi in enumerate(self.x_train):
condition = self.y_train[index] * (np.dot(xi , self.w) - self.b ) >= 1
dw , db = self.gradient(xi, self.y_train[index], condition)
#Update The Weights and The Bias
self.w -= self.learning_rate * dw
self.b -= self.learning_rate * db
def predict(self , x):
y_hat = np.dot(x , self.w) - self.b
return np.sign(y_hat)
def displayTheModel(self,x,y):
fig , ax = plt.subplots()
ax.scatter(x[:,0][y==1] , x[:,1][y==1] , marker='o')
ax.scatter(x[:,0][y==-1] , x[:,1][y==-1] , marker='+')
x0_min = np.amin(x[:,0])
x0_max = np.amax(x[:,0])
x1_x_for_separator = (-self.w[0] * x0_min + self.b + 0 ) / self.w[1]
x1_y_for_separator = (-self.w[0] * x0_max + self.b + 0 ) / self.w[1]
x1_x_for_class1 = (-self.w[0] * x0_min + self.b -1 ) / self.w[1]
x1_y_for_class1 = (-self.w[0] * x0_max + self.b -1 ) / self.w[1]
x1_x_for_class2 = (-self.w[0] * x0_min + self.b + 1 ) / self.w[1]
x1_y_for_class2 = (-self.w[0] * x0_max + self.b + 1 ) / self.w[1]
ax.plot([x0_min , x0_max] , [x1_x_for_separator , x1_y_for_separator] , "red")
ax.plot([x0_min , x0_max] , [x1_x_for_class1 , x1_y_for_class1] , "black")
ax.plot([x0_min , x0_max] , [x1_x_for_class2 , x1_y_for_class2] , "black")
x1_min = np.amin(x[:, 1])
x1_max = np.amax(x[:, 1])
ax.set_ylim([x1_min - 3, x1_max + 3])
plt.show()
def getAccuarcy(self , y_true , y_pred):
return np.sum(y_true == y_pred) / len(y_true)
Testing The Model :
1
2
3
4
5
6
7
8
9
10
11
x , y = make_blobs(n_samples=100 , n_features=2 , centers=2 , random_state=0)
y = np.where(y==0 , -1 , 1)
x_train , x_test , y_train , y_test = train_test_split(x , y , test_size=0.25)
svm = SVM()
svm.fit(x_train, y_train)
svm.train()
y_hat = svm.predict(x_test)
print("Model Accuracy : ",svm.getAccuarcy(y_test, y_hat))
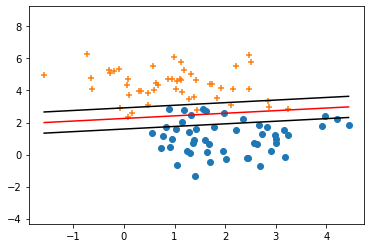
svm.displayTheModel(x, y)
The Model Result :